Gossiping and opinion dynamics in Social Networks

This post is composed by extracts and extensions of a project I started developing when taking the Complex Social Networks course in Fall 2023. I began studying the gossip spread in the giant component of Random Hyperbolic Graphs (RGHs) in the regime when the degree distribution obeys a power law with an exponent in the range (2,3). I focused on the spread’s speed and convergence in comparison to other classic graph models; Erdős–Rényi (ER), Barábasi-Albert (BA), and Watts-Strogartz (WS). Based on the idea that hubs are the main boosters of diffusion, I presented and proved adaptations of ER, BA and WS graph models that present the same average degree that a RGH of the same size in expectation. Of course, their degree distributions still don’t follow a power law, and therefore that first study ended up being an analysis of how such degree distribution and other properties (preferential attachment, small-world phenomena) impact the speed of diffusion.

Is the giant component of a RHG also a RHG?

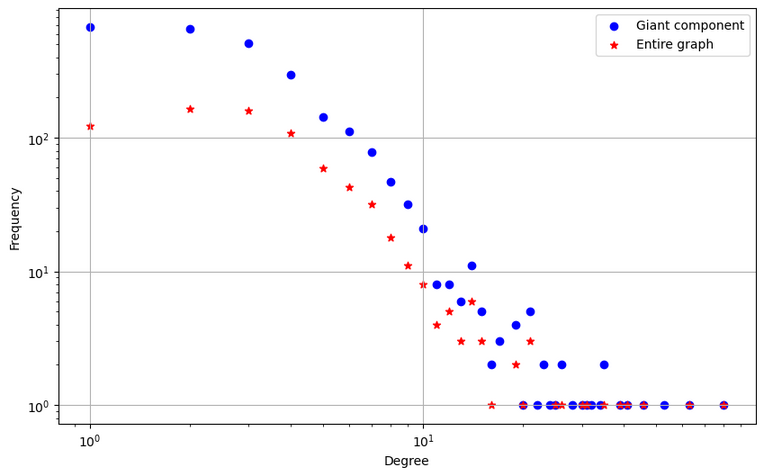
In order to study spread of any kind in a graph, we must first make sure such graph is connected. RGHs often are not connected, but exhibit a giant component that, furthermore, contains all the hub nodes w.h.p.. In the title question, we want to know, does the giant component also obey a power law degree distribution? The following plot shows the degree distribution of a RHG sample for 3000 nodes, \(\nu=1\) and \(\alpha=0.9\)

Gossiping

The gossiping problem was proposed originally as follows (1):

There are \(n\) ladies, and each of them knows some item of gossip not known to the others. They communicate by telephone, and whenever one lady calls another, they tell each other all that they know at that time. How many calls are required before each gossip knows everything?

If we set the number of gossips -and therefore ladies or sources- to \(n=1\), this is equivalent to broadcasting. Now, intuitively, nodes with large degrees, also known as celebrities or influencers, should be the most effective sources of gossip if we want to to optimize the spread speed, right? Were we to want to get a message across a network as quick as possible, it seems natural to choose such sources. But if we are trying to promote our friend’s business, getting a “big” celebrity (one of the nodes with highest degree) to talk about it might be unfeasible, because such person is unreachable. Rather, we could think of contacting a few, less-known micro-celebrities. Maybe if we do that skillfully enough, we might be even able to spread our message even faster than if we contacted the big celebrity to begin with!

We want to focus on this new optimization problem and its dynamics. How many, how popular celebrities would be optimal for our gossiping or broadcasting scenario?

Opinion dynamics

In the previous scenario, we assumed nodes agreed to receive and then spread the message once it gets to them. In a real complex social network, this is unlikely. We can define the cost of getting a node to spread our gossip as their degree. Then, for a graph \(G=(V, E)\) with the typical definition of a node \(v\) neighborhood \(N(v)=\{u\in V \mid (u, v)\in E\}\), its cost \(c: V \to \mathbb{N}\) where \(c(v)=|N(v)|\). This not only affects us as source-placers, but also indicates that in order to get a hub (high-degree node) to spread our gossip, all their neighbors must already know the gossip - or it must be a source -. This might make hubs look useless unless they are sources.

However, in the real world, there are many pieces of gossip being spread at the same time. Some of it might be contrary to ours, so we can try and see in what situations we have some interesting scenarios

• In induced tree structures, leave-parents (this is, nodes which have at least one neighbor with degree 1) will never accept any gossip if at least one of their leave neighbors are not a source.

Proof: Let us name node \(u\) and \(v\) as a leaf and its parent, respectively, such that \(u\subset N(v)\) - note also that \(u \subsetneq N(v)\), and none of them are sources of gossip. Let us also define the set nodes being sources of gossip \(S\). At any given timestep of the process \(t\), \(v\) will accept the gossip for the first time - \(v_{t-1}\notin S\), \(v_t\in S\) - if \(w_{t-1} \in S \forall w \in N(v)\), which implies \(u_{t-1}\in S\). By contradiction, this can’t happen if \(u_0, v_0 \notin S\).

Bibliography

• (1) Brenda Baker. “Gossips and Telephones” Brenda Baker and Robert Shostak Discrete Mathematics 2 (1972) 191–193 The following problem has circuated lately among mathematicians. Other solutions have been given independently by RT Bumby and by A. Hajnal, EC Milner and E. Szemerédi.” In: Discrete Mathematics 2 (1972), pp. 191–193